Степень изменения поисковой выдачи, или на сеошном жаргоне «сила апдейта», давно интересует веб-аналитиков для решения ряда практических задач поисковой оптимизации. Самыми распространёнными из них являются:

• анализ апдейтов поисковых систем;
• задачи управления репутацией;
• анализ конкуренции в нише.

Существует достаточно большое количество сервисов — индикаторов апдейтов — которые мониторят поисковую выдачу и предоставляют информацию о «штормах» и прочей «погоде» на ландшафте поисковых систем. Но, к сожалению, ни один из этих сервисов не раскрывает свой способ расчёта тех самых штормов.
А верить на слово, о том, что именно этот индикатор является самым правильным апдейтом или самым точным апдейтом не получается. Поэтому пришлось разбираться самому и придумывать свой способ расчёта этого показателя.

Формальное описание способа расчёта см. в моей статье на Хабре «Оценка вариативности поисковой выдачи», а здесь я хочу на простых примерах показать, как этот показатель рассчитывается.

Итак, имеем следующую формулу для расчёта взвешенного относительного расстояния между двумя рейтингами R^’ и R^’’

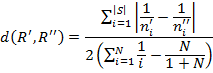
Здесь:
N — длина рейтинга (ТОП5, ТОП10 и т.п.);
|S| — количество элементов в множестве S = R^’ U R^’’, то есть общее количество уникальных объектов в двух рейтингах;
n^’_i и n^’’_i — позиции i-го элемента соответственно в рейтинге R^’ и R^’’, причём если объект отсутствует в рейтинге, то его позиция в этом рейтинге принимается за N+1.

Рассмотрим несколько примеров расчёта степени изменения поисковой выдачи на основе рейтинга ТОП5.

Пример 1. Просто пример расчёта.

Пусть
N = 5, R’ = {a,b,c,d,e}, R’’ = {f,b,c,e,d}.
Тогда
S = {a,b,c,d,e,f}, |S| = 6
da = |1/1-1/(N+1)| = |1-1/6| ≈ 0,83
db = |1/2-1/2| = 0
dc = |1/3-1/3| = 0
dd = |1/4-1/5| =0,05
de = |1/5-1/4| = |-0,05| = 0,05
df = |1/6-1/1| ≈ 0,83
Отсюда числитель ≈ 0,83+0+0+0,05+0,05+0,83 ≈ 1,76
Знаменатель ≈ 2(1/1+1/2+1/3+1/4+1/5-5/6) ≈ 2(2,28-0,83) ≈ 2,9
Откуда d ≈ 0,61.

Пример 2. Замена одного объекта без смещения остальных — имитация замены сайта на его аффилиат.

В первом случае - в начале рейтинга.
N = 5, R’ = {a,b,c,d,e}, R’’ = {f,b,c,d,e}.
Тогда
S = {a,b,c,d,e,f}, |S| = 6
da = df ≈ 0,83
db = dc = dd = de = 0
Числитель ≈ 1,66
Знаменатель ≈ 2,9
d ≈ 0,57

Во втором случае - в конце рейтинга.
N = 5, R’ = {a,b,c,d,e}, R’’ = {a,b,c,d,f}.
Тогда
S = {a,b,c,d,e,f}, |S| = 6
da = db = dc = dd = 0
de = df ≈ 0,03
Числитель ≈ 0,06
Знаменатель ≈ 2,9
d ≈ 0,02

То есть данная метрика весьма чувствительна к месту изменений — чем ближе к концу рейтинга, тем меньше её значение. Это происходит потому, что в качестве весов позиций используется их CTR, который стремительно падает по направлению к концу рейтинга. См. подробнее об этом Кликабельность органической выдачи.

Пример 3. Транспозиция объектов — имитация обмена сайтов местами.

В первом случае - в начале рейтинга.
N = 5, R’ = {a,b,c,d,e}, R’’ = {b,a,c,d,e}.
Тогда
S = {a,b,c,d,e}, |S| = 5
da = db = 0,5
dc = dd = de = 0
Числитель ≈ 1
Знаменатель ≈ 2,9
d ≈ 0,34

Во втором случае - в конце рейтинга.
N = 5, R’ = {a,b,c,d,e}, R’’ = {a,b,c,e,d}.
Тогда
S = {a,b,c,d,e}, |S| = 5
da = db = dc = 0
dd = de = 0,05
Числитель ≈ 0,1
Знаменатель ≈ 2,9
d ≈ 0,03

То есть данная метрика чувствительна и к локальным изменениям (без смены состава ранжируемых объектов).

Вообще, нужно помнить о том, что изменения в поисковой выдаче могут происходить как по причине смены самой функции ранжирования, так и регулярных изменений базы для её расчёта (поискового индекса). Для выявления истинной причины необходима нетривиальная обработка статистики апдейтов, выделение трендов, очистка от статистических шумов… это всё оставим на потом. А сейчас нас интересовал только расчёт именно единичного измерения — чтобы понять, что выпало на нашем «кубике» — единичка или шестёрка (какой силы был тот самый «шторм»).

Да пребудет с нами сила! Сила апдейта.